Exploring Ancient Pythagorean Philosophy
The world of ancient philosophy is a treasure trove of ideas, and at its heart lies the enigmatic figure of Pythagoras. Born on the island of Samos around 570 BCE, Pythagoras is often celebrated for his contributions to mathematics, but his influence extends far beyond that. His philosophy was not just about numbers; it was a comprehensive worldview that intertwined ethics, spirituality, and the very fabric of the universe. Imagine a time when numbers were not merely tools for calculation but held profound mystical significance. This article delves deep into the core tenets of Pythagorean philosophy, its historical context, and the lasting impact it has had on mathematics, science, and spirituality.
Pythagoreanism was more than a mathematical doctrine; it was a way of life. Pythagoras and his followers, known as the Pythagoreans, believed in the interconnectedness of all things. They viewed the universe as a harmonious entity governed by numerical relationships. This perspective led to groundbreaking discoveries not only in mathematics but also in music, ethics, and cosmology. The Pythagorean theorem, which many consider the pinnacle of Pythagorean mathematics, is just the tip of the iceberg. Underneath lies a rich tapestry of ideas that continue to resonate in modern thought.
But what exactly did Pythagoras and his followers teach? Their philosophy can be broken down into several key areas:
- Mathematics: The Pythagoreans established foundational principles of geometry and number theory.
- Music: They discovered the mathematical ratios that underpin musical harmony.
- Ethics: Pythagorean ethics emphasized the importance of living a virtuous life in harmony with the cosmos.
- Cosmology: Their beliefs included ideas about the soul and reincarnation, reflecting a holistic understanding of existence.
As we journey through the realms of Pythagorean thought, we will uncover how these ancient ideas shaped not only the philosophy of the time but also laid the groundwork for future thinkers like Plato. The Pythagorean legacy is a testament to the enduring power of ideas, reminding us that the quest for knowledge is as relevant today as it was over two millennia ago.
In the following sections, we will explore the life of Pythagoras, the mathematical concepts he introduced, and the philosophical beliefs that defined his teachings. We will also examine the profound influence of Pythagoreanism on later philosophical developments and its lasting impact on modern thought. So, buckle up as we embark on this fascinating journey through the ancient world of Pythagorean philosophy!

The Life of Pythagoras
Pythagoras, a name that resonates through the corridors of history, was not just a mathematician; he was a philosopher, a mystic, and a seeker of truth. Born on the island of Samos around 570 BCE, Pythagoras lived during a time when the ancient world was ripe for exploration and discovery. His life was a tapestry woven with threads of intellectual curiosity and spiritual quest, leading him to travel extensively across the Mediterranean, soaking up knowledge from various cultures.
His journey took him to Egypt, where he was introduced to the profound mysteries of mathematics and geometry, as well as to Babylon, where he encountered advanced astronomical concepts. These experiences shaped his worldview and laid the groundwork for his teachings. Pythagoras believed that the universe was governed by mathematical laws, a revolutionary idea that would echo through the ages.
Upon returning to Samos, Pythagoras founded a school that was more than just a place of learning; it was a community of like-minded individuals dedicated to the pursuit of knowledge and the exploration of the cosmos. This community, often referred to as the Pythagorean Brotherhood, adhered to strict rules, including a vegetarian diet and communal living. They believed in the transmigration of the soul, which emphasized the importance of ethical living and the quest for personal enlightenment.
One of the most fascinating aspects of Pythagoras's life was his belief in the mystical significance of numbers. He famously stated, "All is number," which encapsulated his philosophy that numbers were the essence of all things. The Pythagoreans viewed numbers not just as mathematical entities, but as symbols with deep spiritual meaning. For instance, they associated the number one with unity and the divine, while the number two represented duality and balance.
His teachings extended beyond mathematics into ethics and cosmology, creating a holistic approach to knowledge that emphasized the interconnection of all things. Pythagoras's influence was profound, and his ideas laid the foundation for later philosophical inquiries. His emphasis on reason and rationality would later resonate with philosophers like Plato, who admired Pythagorean thought and integrated many of its principles into his own philosophy.
In summary, Pythagoras was a remarkable figure whose life and teachings transcended the boundaries of mathematics and philosophy. His legacy continues to inspire scholars and thinkers, reminding us of the profound connections between numbers, the universe, and the human experience. As we delve deeper into the realms of Pythagorean thought, we uncover not just the principles of mathematics but also a way of viewing the world that emphasizes harmony, balance, and the pursuit of knowledge.
- Who was Pythagoras? Pythagoras was an ancient Greek philosopher and mathematician known for his contributions to mathematics, particularly the Pythagorean theorem.
- What did Pythagoras believe about numbers? Pythagoras believed that numbers had mystical significance and were the foundation of all reality.
- What is the Pythagorean Brotherhood? The Pythagorean Brotherhood was a community founded by Pythagoras that focused on philosophy, mathematics, and ethical living.
- How did Pythagoras influence later philosophers? Pythagoras's ideas about mathematics and ethics significantly influenced later philosophers, including Plato, who integrated many Pythagorean concepts into his work.

Pythagorean Mathematical Concepts
The realm of Pythagorean mathematics is a fascinating tapestry woven with threads of numbers, shapes, and profound philosophical insights. At the heart of this ancient school of thought lies the famous Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. However, the theorem is merely the tip of the mathematical iceberg that Pythagoras and his followers explored. Their approach to mathematics was not just about numbers; it was a holistic pursuit that intertwined mathematics with the very fabric of reality.
The Pythagoreans viewed numbers as more than mere symbols; they believed that numbers had mystical significance. This belief stemmed from their understanding of numerical relationships and how these relationships reflected the harmony of the universe. For them, numbers were the building blocks of existence, and through them, one could decipher the secrets of the cosmos. They categorized numbers into various types, such as perfect numbers (numbers that are equal to the sum of their proper divisors), amicable numbers (two numbers where each is the sum of the proper divisors of the other), and triangular numbers (numbers that can form an equilateral triangle). Each category held its own significance, further enriching their mathematical framework.
To illustrate the Pythagorean view of numbers, consider the following table that summarizes some of these special categories:
| Type of Number | Description | Example |
|---|---|---|
| Perfect Number | A number equal to the sum of its proper divisors | 6 (1 + 2 + 3 6) |
| Amicable Numbers | Two numbers where each is the sum of the proper divisors of the other | 220 and 284 |
| Triangular Number | A number that can form an equilateral triangle | 3 (1 + 2) |
Moreover, the Pythagoreans were pioneers in exploring the relationships between numbers and musical harmony. They discovered that musical intervals could be expressed through simple numerical ratios. For instance, the octave corresponds to a frequency ratio of 2:1, while a perfect fifth corresponds to a ratio of 3:2. This discovery not only enriched their understanding of music but also reinforced their belief in the interconnectedness of mathematics and the universe. Pythagoras famously stated, "All is number." This phrase encapsulates the essence of Pythagorean thought, where the language of numbers was seen as the key to unlocking the mysteries of existence.
In addition to their work in numerical relationships, the Pythagoreans made significant contributions to geometry. They explored the properties of shapes, particularly triangles and polygons, and established principles that would lay the groundwork for future mathematical discoveries. The concept of geometric proofs was revolutionized by their systematic approach, which emphasized logical reasoning and deduction. For example, the Pythagorean theorem itself is a geometric statement that has been proven in numerous ways throughout history, showcasing the enduring legacy of their geometric explorations.
In summary, the Pythagorean mathematical concepts are a testament to the profound insights of Pythagoras and his followers. Their innovative approaches to numbers, musical harmony, and geometry not only advanced the field of mathematics but also shaped the philosophical landscape of their time. As we delve deeper into the world of Pythagoreanism, we uncover a rich legacy that continues to influence modern thought and scientific inquiry.
- What is the Pythagorean theorem? The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
- What are perfect numbers? Perfect numbers are those that are equal to the sum of their proper divisors, such as 6 and 28.
- How did Pythagoras connect mathematics and music? Pythagoras discovered that musical intervals could be expressed through numerical ratios, illustrating the harmony between mathematics and music.

Numerical Relationships
The Pythagoreans held a profound belief that numbers were not merely tools for counting or measuring but were, in fact, the very essence of the universe. They viewed numbers as possessing mystical significance, which played a crucial role in understanding the world around them. This perspective led them to explore various numerical relationships, emphasizing the connections between numbers, harmony, and the cosmos. One of the most fascinating aspects of their philosophy was the idea that numbers could express the fundamental principles of nature and existence.
At the heart of Pythagorean thought was the concept of harmony. The Pythagoreans believed that harmony could be found in the relationships between numbers, much like the harmony found in music. They discovered that certain numerical ratios produced pleasing sounds, leading them to conclude that the universe itself was governed by similar harmonious principles. For example, when they examined the ratios of string lengths that produced harmonious musical intervals, they found that:
| Interval | Ratio | Example |
|---|---|---|
| Octave | 2:1 | Doubling the string length |
| Perfect Fifth | 3:2 | String length ratio of 3 to 2 |
| Perfect Fourth | 4:3 | String length ratio of 4 to 3 |
Through these discoveries, the Pythagoreans established a profound connection between mathematics and music, showcasing how numerical relationships could transcend mere calculations and enter the realm of aesthetic experience. They believed that understanding these ratios not only enhanced musical performance but also offered insights into the very fabric of reality.
Furthermore, the Pythagoreans explored the concept of proportion as a means of understanding the world. They recognized that proportions were essential in various aspects of life, from architecture to art, and even in the movements of celestial bodies. By studying the relationships between different numbers, they sought to uncover the underlying order of the universe. This quest for understanding led to the development of the idea of mathematical ratios, which became foundational in later mathematical theories.
The Pythagorean understanding of numerical relationships also extended to the concept of even and odd numbers. They believed that even numbers represented harmony and stability, while odd numbers symbolized chaos and imbalance. This dichotomy influenced their worldview, as they sought to find balance in all aspects of existence. The significance of these numerical relationships was not just theoretical; it shaped their ethical beliefs and their understanding of the cosmos.
In summary, the Pythagorean exploration of numerical relationships was a groundbreaking endeavor that intertwined mathematics, music, and philosophy. Their belief that numbers held profound meaning not only influenced their own society but also laid the groundwork for future generations of thinkers. By recognizing the harmony and proportion inherent in numbers, the Pythagoreans opened the door to a deeper understanding of the universe and our place within it.
- What is the significance of numerical relationships in Pythagorean philosophy?
Numerical relationships were viewed as the key to understanding the universe, connecting mathematics, music, and the natural world. - How did Pythagoreans relate numbers to music?
Pythagoreans discovered that specific numerical ratios corresponded to musical intervals, demonstrating a profound connection between mathematics and harmony. - What role did even and odd numbers play in Pythagorean thought?
Even numbers represented harmony and stability, while odd numbers symbolized chaos, influencing their ethical beliefs and worldview.

Harmony in Music
The connection between mathematics and music is not just a coincidence; it's a profound relationship that Pythagoras and his followers explored deeply. Pythagoras famously stated that "all is number," and this mantra resonated through his investigations into the world of sound. He discovered that musical harmony can be expressed through simple mathematical ratios, revealing an underlying order in what might seem like chaos. For instance, when two strings vibrate, the ratio of their lengths determines the harmony of the sounds they produce. This idea is encapsulated in the following ratios:
| Interval | Ratio | Example |
|---|---|---|
| Octave | 2:1 | When a string is halved |
| Perfect Fifth | 3:2 | When one string is 1.5 times longer than another |
| Perfect Fourth | 4:3 | When one string is 1.33 times longer than another |
This mathematical foundation of music was revolutionary. Pythagoras’s exploration led to the understanding that different sounds could be organized into a coherent structure, much like how numbers can be arranged. Imagine tuning a guitar: each string must be adjusted to match a specific frequency, and this adjustment is fundamentally a mathematical process. The Pythagorean approach to music was not merely academic; it was a spiritual and philosophical pursuit. Music was seen as a way to connect with the cosmos, reflecting the harmony of the universe itself.
Moreover, the Pythagorean belief in the significance of harmonics extended beyond music theory. They viewed harmonious sounds as a representation of cosmic order, suggesting that the universe itself is governed by mathematical principles. This belief led to the idea that understanding music could lead to a greater understanding of the universe and our place within it. In essence, the Pythagoreans believed that by studying music, one could tap into the very essence of existence.
In summary, the Pythagorean insights into the relationship between music and mathematics laid the groundwork for future explorations in both fields. Their discoveries not only enriched the understanding of musical theory but also painted a broader picture of how interconnected everything is—from the strings of a musical instrument to the very fabric of the universe.
- What is the significance of Pythagorean ratios in music?
Pythagorean ratios help define the intervals in music, establishing a mathematical basis for harmony. - How did Pythagoras contribute to our understanding of music?
Pythagoras discovered that musical notes correspond to specific mathematical ratios, influencing both music theory and philosophy. - Can the principles of Pythagoreanism be applied to modern music?
Yes, many modern musical compositions still utilize the mathematical ratios identified by Pythagoras to create harmony.
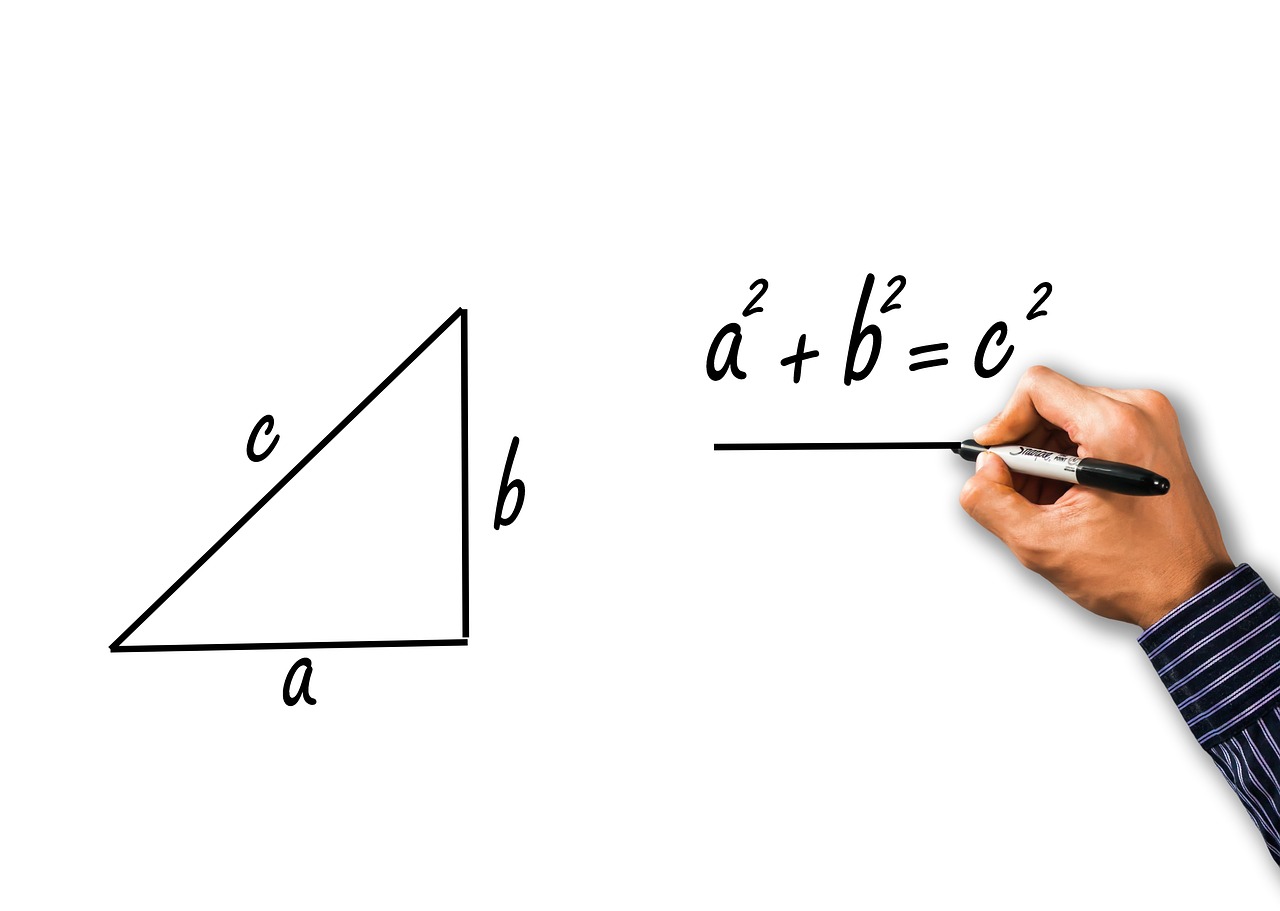
Geometric Discoveries
The Pythagoreans were not just mathematicians; they were also profound thinkers who laid the groundwork for geometry as we know it today. Their explorations into shapes, lines, and angles were revolutionary, allowing them to unlock the secrets of the universe through mathematical principles. One of the most significant contributions attributed to Pythagoras is the understanding of right triangles, encapsulated in the famous Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This relationship is not just a formula; it’s a gateway into understanding the very fabric of space.
But Pythagorean discoveries went far beyond just right triangles. They delved into the properties of various polygons and their angles, establishing foundational rules that would be taught for centuries. For instance, they recognized that the sum of the interior angles of a triangle is always 180 degrees. Such insights were not merely academic; they had practical applications in architecture, astronomy, and even in navigation. Can you imagine how these early geometric principles influenced the construction of the grand temples and structures of ancient Greece?
Moreover, the Pythagoreans classified shapes into categories based on their properties. They noted the differences between regular polygons, which have equal sides and angles, and irregular ones, which do not. This classification helped to create a systematic approach to geometry that would later be expanded upon by Euclid and other mathematicians.
Another fascinating aspect of Pythagorean geometry was their exploration of the concept of irrational numbers. When they discovered that the diagonal of a square could not be expressed as a ratio of two whole numbers, they were confronted with a mathematical crisis that challenged their belief in the harmony of numbers. This realization led to a deeper understanding of numbers and their relationships, paving the way for future mathematical discoveries.
To illustrate some of the key geometric discoveries made by the Pythagoreans, consider the following table:
| Geometric Concept | Description |
|---|---|
| Pythagorean Theorem | The relationship between the sides of a right triangle: a² + b² c². |
| Sum of Angles in a Triangle | The sum of the interior angles of a triangle is always 180 degrees. |
| Classification of Polygons | Regular polygons have equal sides and angles; irregular polygons do not. |
| Irrational Numbers | Discovery that some lengths, such as the diagonal of a square, cannot be expressed as a ratio of integers. |
In conclusion, the geometric discoveries of the Pythagoreans were not merely academic exercises; they were a profound exploration of the universe's underlying order. Their work laid the groundwork for future generations, influencing not only mathematics but also philosophy, art, and science. Just like a master sculptor chisels away at a block of marble to reveal a beautiful statue, the Pythagoreans carved out the fundamental principles of geometry that continue to shape our understanding of the world today.
- What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. - How did Pythagoras influence modern mathematics?
Pythagoras laid the groundwork for geometry, introducing concepts that are still taught today, such as the properties of triangles and the classification of polygons. - What are irrational numbers?
Irrational numbers are numbers that cannot be expressed as a ratio of two integers. The discovery of such numbers by the Pythagoreans challenged their beliefs about the harmony of numbers.

Philosophical Beliefs
Pythagorean philosophy extends far beyond the realm of mathematics; it embraces a rich tapestry of ethical principles, cosmological views, and profound beliefs about the nature of existence. Central to their philosophy is the idea that the universe is governed by mathematical relationships, which reflects a deeper cosmic order. For Pythagoreans, understanding these relationships was not merely an intellectual exercise but a pathway to achieving harmony within oneself and with the universe.
One of the most intriguing aspects of Pythagorean thought is their belief in the immortality of the soul. They posited that the soul undergoes a cycle of reincarnation, where it is reborn into different forms of life based on its previous actions. This belief in metempsychosis encouraged a lifestyle of ethical living and self-discipline, as each individual was seen as responsible for their own spiritual evolution. The Pythagoreans believed that by living virtuously, one could purify the soul and ultimately achieve a state of enlightenment.
Moreover, the Pythagoreans viewed the universe as a living entity, imbued with a divine order that could be understood through mathematical principles. They believed that by studying numbers and their relationships, one could uncover the fundamental truths of existence. This belief is beautifully encapsulated in their famous saying, "All is number." For them, numbers were not just symbols, but the very essence of reality, connecting the physical world with the metaphysical.
The Pythagorean worldview also encompassed a strong sense of community and brotherhood. Their society was structured around shared beliefs and practices, which fostered a sense of belonging and mutual support among its members. They adhered to strict rules, including dietary restrictions and communal living, as a means of cultivating both personal discipline and collective harmony. This emphasis on community was not just practical; it was a reflection of their belief that individual souls were interconnected within the greater cosmic fabric.
In summary, the philosophical beliefs of the Pythagoreans represent a fascinating intersection of mathematics, ethics, and spirituality. Their teachings continue to resonate today, inviting us to ponder our own existence and the underlying principles that govern our lives. As we explore the legacy of Pythagorean thought, we uncover a profound understanding of the universe that is as relevant now as it was in ancient times.
- What is the main belief of Pythagorean philosophy?
Pythagorean philosophy centers around the idea that the universe is fundamentally mathematical, and understanding these mathematical relationships can lead to spiritual enlightenment. - Did Pythagoreans believe in reincarnation?
Yes, Pythagoreans believed in the immortality of the soul and the concept of metempsychosis, where the soul is reborn into new forms based on its past actions. - How did Pythagorean philosophy influence later thinkers?
Pythagorean ideas significantly impacted philosophers like Plato, shaping their thoughts on mathematics, ethics, and the nature of reality.

The Influence of Pythagoreanism
Pythagoreanism, with its rich tapestry of mathematical, philosophical, and spiritual ideas, has left an indelible mark on the course of Western thought. Its influence extends far beyond the confines of ancient Greece, permeating various fields such as mathematics, philosophy, and even the arts. The Pythagorean belief that numbers are the essence of all things resonates deeply with many subsequent thinkers, suggesting a profound connection between the universe and numerical relationships.
One of the most notable figures influenced by Pythagoreanism was Plato. He adopted many Pythagorean ideas, integrating them into his own philosophical framework. For Plato, the world of forms—an abstract realm of perfect ideals—was inherently mathematical. This perspective not only shaped his philosophical inquiries but also laid the groundwork for future philosophical discourse. The Pythagorean emphasis on harmony and proportion found its way into Plato's theories, particularly in his explorations of ethics and aesthetics.
The impact of Pythagorean thought can also be seen in the development of scientific ideas during the Renaissance. Thinkers such as Galileo and Kepler were inspired by the Pythagorean view of the cosmos, where celestial bodies moved in accordance with mathematical principles. This connection between mathematics and the natural world fostered a spirit of inquiry that propelled scientific advancements. The Pythagorean notion that the universe is ordered and can be understood through mathematics became a foundational tenet of modern science.
Moreover, the Pythagorean legacy is not limited to mathematics and philosophy; it has also found expression in the arts. The idea that beauty can be quantified through mathematical ratios has influenced artists and musicians throughout history. For example, the Pythagorean discovery of musical intervals based on numerical ratios revolutionized the way music was composed and perceived. This profound connection between mathematics and music continues to inspire contemporary artists and musicians alike.
In contemporary times, Pythagorean principles are still relevant. The concept of mathematical beauty—the idea that mathematical equations and theorems possess an aesthetic quality—can be traced back to Pythagorean thought. Modern mathematicians often speak of the elegance of a proof or the beauty of a mathematical structure, echoing the Pythagorean belief in the harmony of numbers. Furthermore, the resurgence of interest in holistic approaches to education and philosophy reflects the Pythagorean ideal of integrating knowledge across disciplines.
As we explore the enduring legacy of Pythagoreanism, it becomes clear that its influence is woven into the very fabric of our intellectual heritage. From the realms of mathematics and science to the arts and philosophy, the ideas of Pythagoras and his followers continue to inspire and challenge us. They remind us that the pursuit of knowledge is not merely an academic endeavor but a holistic journey that encompasses the beauty and mystery of existence.
- What is Pythagoreanism? Pythagoreanism is a philosophical and religious system founded by Pythagoras, emphasizing the importance of numbers, mathematics, and their connection to the cosmos.
- How did Pythagoreanism influence Plato? Plato was heavily influenced by Pythagorean ideas, particularly in his theories of forms, ethics, and the mathematical structure of reality.
- What is the significance of numbers in Pythagorean thought? Pythagoreans believed that numbers had mystical significance and were the key to understanding the universe, embodying harmony and proportion.
- How is Pythagoreanism relevant today? Pythagorean principles continue to resonate in modern mathematics, science, and the arts, influencing contemporary thought and holistic approaches to knowledge.

Pythagoreanism and Plato
Pythagoreanism played a crucial role in shaping the philosophical landscape of ancient Greece, particularly influencing the great philosopher Plato. The intertwining of Pythagorean thought with Plato’s ideas is not just a historical footnote; it represents a significant shift in the way philosophy approached the realms of mathematics, ethics, and metaphysics. Imagine a world where numbers and forms were not merely tools for calculation but were seen as the very essence of reality! This was the world that Pythagoras and his followers envisioned, and it captivated Plato deeply.
Plato, inspired by the Pythagorean belief that the universe is fundamentally mathematical, incorporated these principles into his own philosophical framework. For instance, he embraced the idea that abstract forms or ideas are more real than the objects we perceive with our senses. This notion mirrors the Pythagorean view that numbers and their relationships form the basis of all existence. Plato famously stated, “The unexamined life is not worth living,” which resonates with the Pythagorean commitment to a life of inquiry and understanding.
One of the most significant ways in which Pythagoreanism influenced Plato was through the concept of harmony. The Pythagoreans believed that harmony in music could be expressed mathematically, and Plato extended this idea to the cosmos. He suggested that the universe itself operates according to mathematical principles, which is akin to the Pythagorean belief that the cosmos is structured in a harmonious way. In Plato’s work, particularly in his dialogue The Republic, we see a reflection of this idea where he discusses the role of mathematics in understanding justice and the ideal state.
To illustrate the profound impact Pythagoreanism had on Plato, consider the following table that highlights key concepts shared between the two:
| Pythagorean Concept | Plato's Interpretation |
|---|---|
| Mathematical Reality | Abstract Forms as the essence of reality |
| Harmony and Order | The cosmos operates in a harmonious manner |
| Reincarnation of the Soul | Immortality and the journey of the soul towards knowledge |
| Ethics grounded in Knowledge | Virtue as a form of knowledge |
Moreover, the Pythagorean emphasis on ethical living influenced Plato's notion of the philosopher-king, a ruler who possesses knowledge and wisdom. In Plato’s ideal society, those who govern must understand the higher truths of existence, much like the Pythagoreans who believed that knowledge leads to a virtuous life. This connection underscores the idea that philosophy is not merely an intellectual pursuit but a way of life that demands ethical considerations.
In conclusion, the relationship between Pythagoreanism and Plato is a fascinating study of how ancient philosophies intertwined to shape Western thought. Plato’s works reflect a deep appreciation for the mathematical and ethical insights provided by the Pythagoreans, and their legacy continues to influence contemporary philosophical discussions. The idea that numbers, harmony, and ethics are interconnected remains a powerful testament to the enduring nature of Pythagorean philosophy.
- What is Pythagoreanism? Pythagoreanism is a philosophical and religious school of thought founded by Pythagoras, emphasizing the significance of numbers, mathematics, and harmony in understanding the universe.
- How did Pythagoras influence Plato? Pythagoras influenced Plato through concepts of mathematical reality, harmony, and the ethical implications of knowledge, which Plato integrated into his own philosophical framework.
- What is the relationship between mathematics and philosophy in Pythagorean thought? Pythagorean thought posits that mathematics is fundamental to understanding reality, with numbers and their relationships serving as the basis for both the physical and metaphysical worlds.

Legacy in Modern Thought
The legacy of Pythagorean philosophy is not just a relic of the past; it is a vibrant thread woven through the fabric of modern thought. Pythagoras and his followers introduced ideas that transcended their time, laying the groundwork for various fields, including mathematics, science, and even spirituality. Their belief that numbers and mathematical relationships underpin the universe has echoed through the ages, influencing thinkers from ancient Greece to contemporary scientists.
One of the most profound impacts of Pythagoreanism is evident in the realm of mathematics. The Pythagorean theorem, a fundamental principle in geometry, serves as a cornerstone in both education and practical applications. It's fascinating to think that this ancient discovery continues to find relevance in fields such as architecture, engineering, and even computer science. The simplicity and elegance of the theorem demonstrate how Pythagorean thought has permeated modern methodologies.
Moreover, the Pythagorean approach to numerical relationships, emphasizing harmony and proportion, resonates in various disciplines. For instance, in music theory, the mathematical ratios that define musical intervals can be traced back to Pythagorean ideas. Musicians and composers today still rely on these principles to create harmonious compositions, illustrating how Pythagorean beliefs have shaped artistic expression.
In addition to mathematics and music, Pythagorean philosophy has influenced the scientific method itself. The idea that the universe is governed by rational principles laid the groundwork for later scientific inquiry. Thinkers like Galileo and Newton, who sought to understand the laws of nature, were undoubtedly inspired by the Pythagorean notion that the cosmos is orderly and comprehensible through mathematics. This connection between Pythagorean thought and the scientific revolution cannot be overstated.
Furthermore, Pythagoreanism has left its mark on philosophical discourse, particularly in the realm of ethics and metaphysics. The Pythagorean belief in the immortality of the soul and the concept of reincarnation have sparked discussions that continue to this day. Modern philosophies that explore consciousness, existence, and the nature of reality often reflect Pythagorean influences, demonstrating that these ancient ideas remain relevant in contemporary debates.
To summarize the enduring impact of Pythagorean philosophy, we can outline its key contributions to modern thought:
- Mathematics: The Pythagorean theorem and the study of numerical relationships.
- Music: The connection between mathematical ratios and musical harmony.
- Science: The foundation for scientific inquiry and the search for universal laws.
- Philosophy: Discussions on the soul, ethics, and the nature of existence.
In conclusion, the legacy of Pythagorean philosophy is a testament to the power of ideas. Its influence can be seen in the very structures of our modern world, from the buildings we inhabit to the music we enjoy and the scientific principles we uphold. The Pythagorean belief that the universe is a harmonious whole continues to inspire and challenge us, urging us to seek knowledge and understanding in every aspect of our lives.
1. What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. It's expressed as a² + b² c².
2. How did Pythagorean philosophy influence modern science?
Pythagorean philosophy emphasized that the universe operates on rational principles, which laid the groundwork for the scientific method and influenced later scientists like Galileo and Newton.
3. What are some Pythagorean contributions to music?
Pythagoreans discovered that musical intervals can be expressed as mathematical ratios, which has shaped the foundation of music theory and composition.
4. Are Pythagorean beliefs still relevant today?
Yes, Pythagorean beliefs continue to influence modern thought in various fields, including mathematics, music, science, and philosophy, reflecting their timeless nature.
Frequently Asked Questions
- What are the core tenets of Pythagorean philosophy?
Pythagorean philosophy is built on the belief that numbers and mathematical relationships are fundamental to understanding the universe. It encompasses various aspects such as ethics, cosmology, and the pursuit of knowledge, emphasizing the interconnectedness of all things through numerical harmony.
- How did Pythagoras influence mathematics?
Pythagoras is best known for the Pythagorean theorem, but his contributions extend far beyond that. He and his followers explored numerical relationships, ratios, and geometric principles, laying the groundwork for modern mathematics and influencing later thinkers like Plato.
- What is the significance of harmony in Pythagorean thought?
Harmony was central to Pythagorean philosophy, particularly in music and mathematics. Pythagoreans believed that numerical ratios could explain musical intervals, reflecting a deeper cosmic order. This connection between music and math illustrates their belief in harmony as a universal principle.
- Did Pythagoreanism have an impact on later philosophical ideas?
Absolutely! Pythagoreanism significantly influenced later philosophers, especially Plato. Many of Plato’s ideas about forms, ethics, and mathematics were shaped by Pythagorean concepts, demonstrating the enduring legacy of Pythagorean thought in Western philosophy.
- What are some key geometric discoveries attributed to Pythagoras?
Pythagoras and his followers made several important geometric discoveries, including the properties of triangles and polygons. Their work laid the foundation for later developments in geometry, influencing mathematicians for centuries to come.
- How does Pythagorean philosophy relate to modern thought?
Pythagorean principles continue to resonate in contemporary mathematics, science, and philosophy. Concepts like numerical relationships, harmony, and the interconnectedness of knowledge remain relevant, illustrating the lasting impact of Pythagorean thought on modern intellectual pursuits.



















